谱元法 Spectrum-Element Method 初探与 Python 演示实现

2020.08.18

在前文中，进行了谱元法的基础之一——伪谱法的初步探索。前文中使用傅里叶级数作为基函数与均匀间隔配点对伪谱法进行实现。本文将继续介绍谱元法的详细推导以及初步实现。

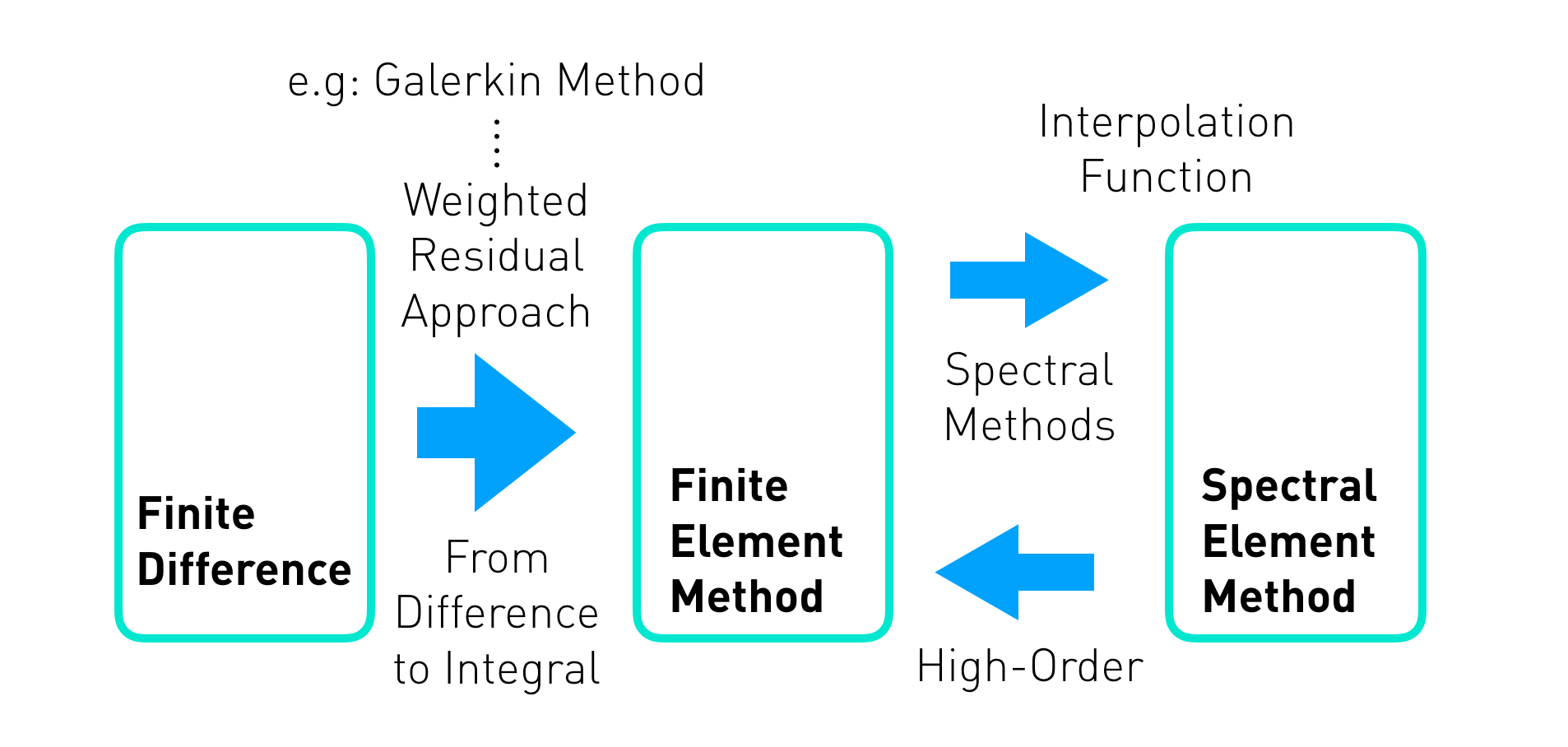
有限差分FDM、有限元FEM与谱元法SEM

对于偏微分方程，例如波动方程等，有限差分的方法是通过泰勒展开在均匀的网格上进行计算。

有限元则是通过加权余量法通过积分方法去计算微分方程的近似解。

SEM可以被认为在有限元方法的基础上使用了更高阶的插值函数（类似于伪谱法）从而得到更高的计算进度的方法。

在传统的有限单元法中，表征单元特性的函数表达式一般都选用低阶的Lagrange插值多项式做基函数，而在谱元法中则常选用高阶的Lagrange插值多项式做基函数。这是谱元法与有限单元法的主要区别。一般认为选用4-8阶Lagrange多项式作为基函数能很好地保证计算的精度和稳定性。 —— 《地震动模拟中的谱元法》

基础知识

为什么要插值？因为要求近似积分。 —— 使用插值函数代替被积函数求解积分为什么要求积分？因为要用积分方法等效计算微分。 —— 加权余量法

在推导之前，先对用到的数学工具进行介绍。

Methods of mean weighted residuals 加权余量法

相较于 Python 中的鸭子类型 Duck Typing：

如果一个东西看起来像个鸭子，游泳像个鸭子，叫声像个鸭子，那么他就是个鸭子。 —— James Whitcomb Riley

那么弱形式就可以被认为，如果一个解左看像真解，右看像真解，那么我们就当它是真解。

通过权函数在有限求解区域上进行加权积分求解满足偏微分方程解的条件，从而得到「弱」满足偏微分方程解的「弱解」。即将偏微分方程有强形式转换成弱形式，从而达到求解偏微分方程的目的。相比于强形式，弱形式的解为求解域上的一个近似解（仅加权平均满足原方程，并非每个点上都满足）

一个简单的例子，对于偏微分方程：

$$ \frac{\partial q(x)}{\partial x} = 0$$

我们可以使用权函数 $v(x)$ 在一段区域上进行积分

$$ \int_\Omega \frac{\partial q(x)}{\partial x} v(x) dx = 0 $$

上式的解不一定是原方程的解，但使用不同的多个权函数的加权积分也等于 $0$，同样也可以被认为是原方程的解。

基函数 vs. 权函数

基函数（试函数、形函数）用于叠加而在选择的若干点上对原函数进行插值（即满足若干点上与原函数相同的情况下对原函数进行重构替换）

权函数则是在上文加权积分中所使用的权值函数。

Galerkin 伽辽金法选择基函数相同的形式的权函数，故二者经常经常被混淆。

如何提高弱解的精确度？使用一组正交的基函数 $v$ ，使用足够多的离散点（离散基函数）。

在本文中介绍的谱元法中，使用Lagrange Integration 拉格朗日插值作为基函数与权函数。

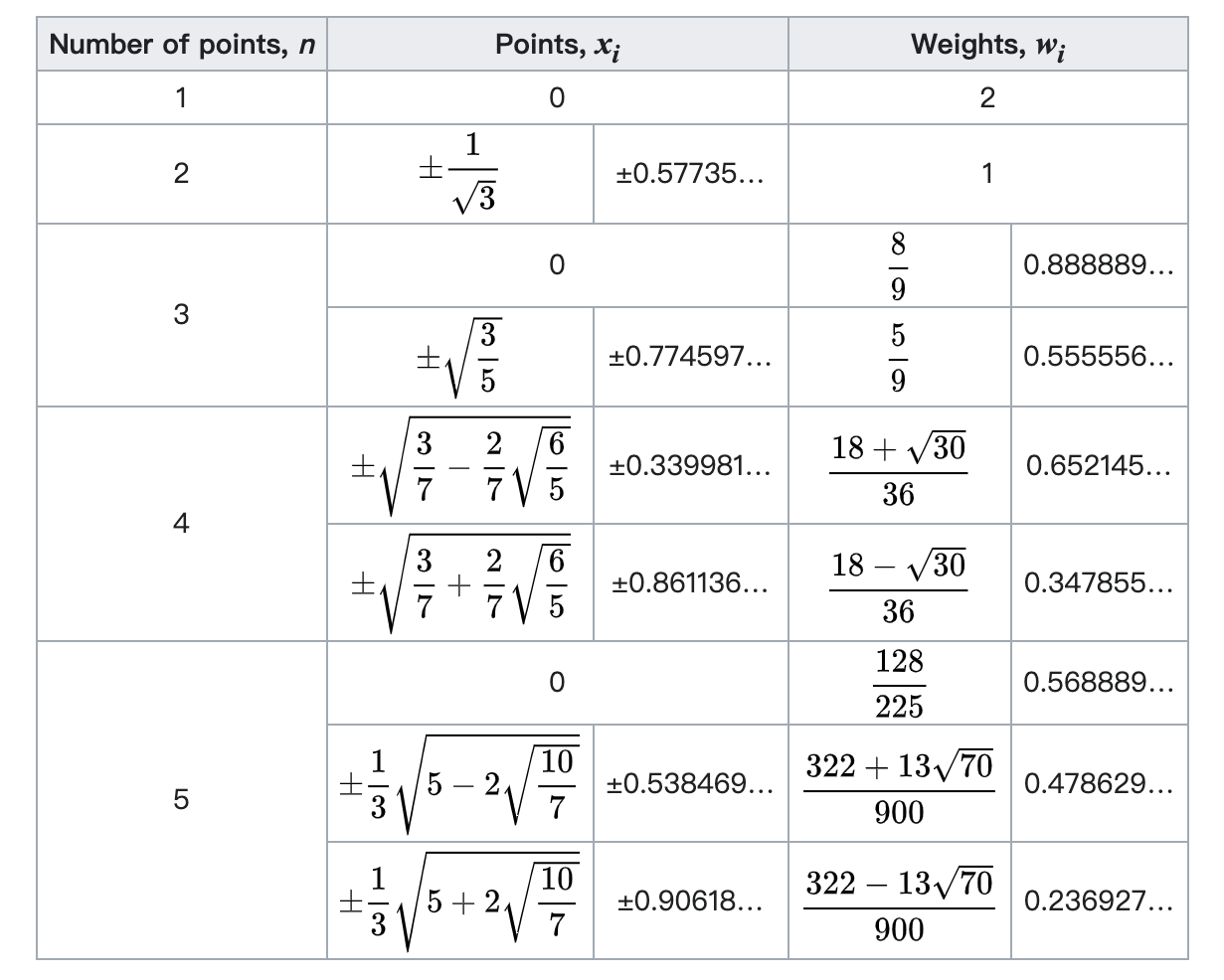
Gauss-Legendre 高斯-勒让德求积方法

对于 $[-1,1]$ 区的函数积分：

$$ \int^1_{-1} f(x) dx$$

其数值解可以由

$$ \sum^n_{i=1} w_i f(x_i)$$

近似计算，其中$f(x_i)$ 为离散点 $x_i$ 对应的函数取值， $w_i$ 为每一项对应的权重。

$$ \int^1_{-1} f(x) dx \approx \sum ^n _{i=1} w_i f(x_i) $$

高斯-勒让德求积方法使用 Legendre 多项式作为基函数且配点的近似求积分方法，以达到最高的代数精度。

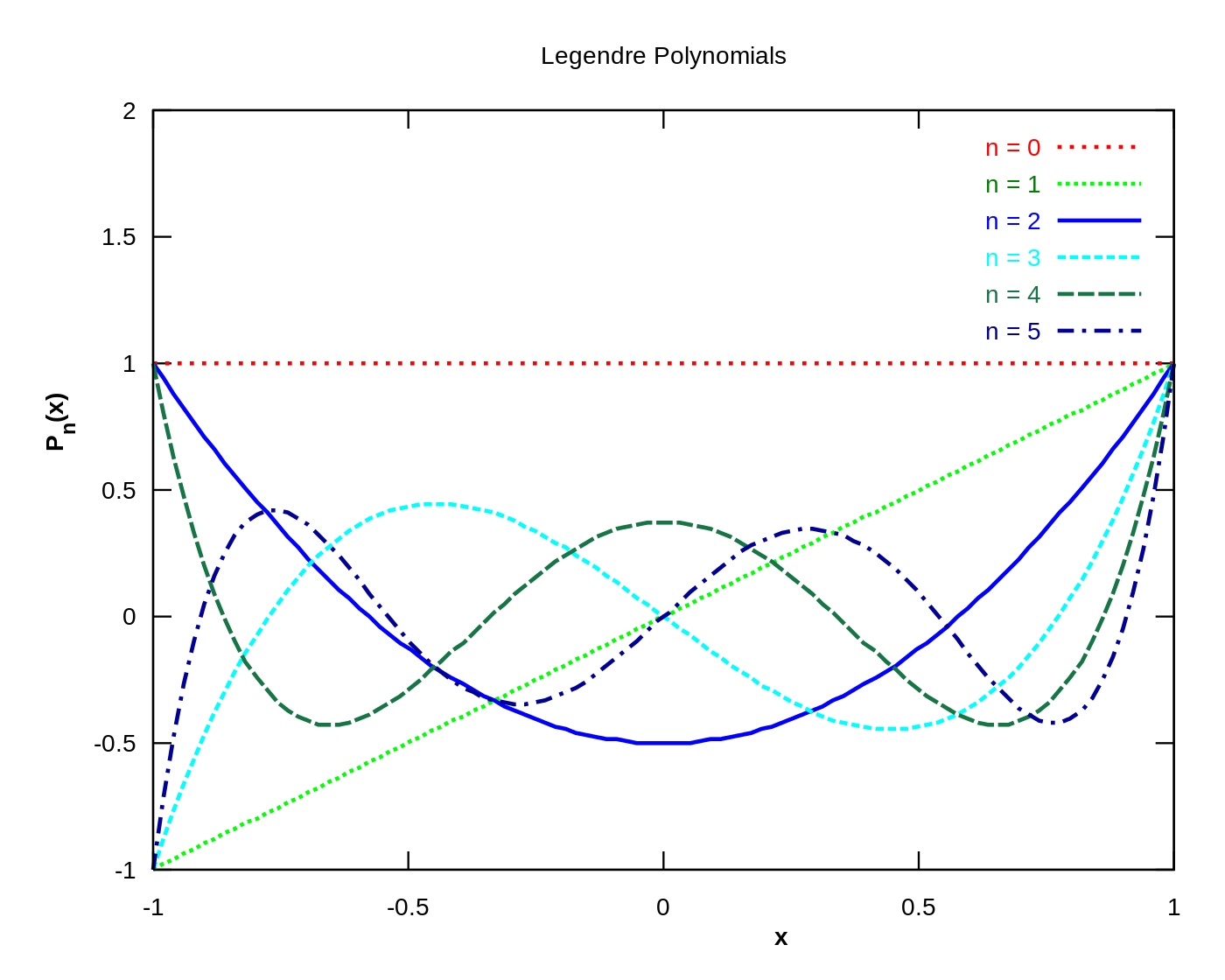
Legendre 多项式及配点方法

满足在 $[-1,1]$ 区间内$P_n(1) = 1$ 的 $n$ 阶 Legendre 多项式的零点，即 Gauss-Lobatto-Legendre points

$$P_n(x) = {1 \over 2^n n!} {d^n \over dx^n } \left[ (x^2 -1)^n \right]$$

前 $6$ 阶Legendre多项式及其零点：

通常情况下往往不满足 $[-1,1]$ 区间范围，可以使用线性变换方法：

$$x = \frac{a+b}{2}+\frac{b-a}{2}t$$

将 $[a, b]$ 区间转换为 $[-1,1]$ 区间。

对于每个配点值积分时的权值为：

$$ \omega_i = \frac{2}{\left( 1 - x_i^2 \right) \left[P’_n(x_i)\right]^2}$$

因为计算量较大，所以一般配点值和权值都事先计算好而后使用时直接查表：

插值形函数：Lagrange Integration 拉格朗日插值

对于$k+1$个点$(x_0,y_0), …, (x_k, y_k)$ 存在总是过这几个点的函数：

$$ L(x) = \sum^k_{j = 0}{y_j\ell_{j}(x)}$$

其中 $y_j$ 直接对应点集合中的每一个点中 $y_j$ 的取值；

每一项 $\ell_{j}(x)$ 函数可以被视为「开关」，当$x = x_j$时 $l_{j}(x) = 1$；而$x \neq x_j$ （即对于其他点）时$\ell_{j}(x) = 0$，类似于克罗内克δ函数，表达式为：

$$\ell_j(x) := \prod_{i=0,, i\neq j}^{k} \frac{x-x_i}{x_j-x_i} = \frac{(x-x_0)}{(x_j-x_0)} \cdots \frac{(x-x_{j-1})}{(x_j-x_{j-1})} \frac{(x-x_{j+1})}{(x_j-x_{j+1})} \cdots \frac{(x-x_{k})}{(x_j-x_{k})}$$

满足：

$$ \ell_i(\xi_j)=\delta_{ij}$$

类比于在前文中使用了傅里叶级数作为基函数：

$$s_N(x) = \sum_{n=-N}^N c_n\cdot e^{i \tfrac{2\pi nx}{P}}$$

都是由一组函数的加和组成的数据描述方法，这一组函数被即被称为基函数

Jacobi matrix 雅克比矩阵

对于从向量 $x$ （$x\inℝ^n$）到向量 $f(x)$ （$f(x)\inℝ^m$）的线性映射，有 $m\times n$ Jacobi 矩阵：

$$\mathbf {J}= \begin{bmatrix} \dfrac{\partial \mathbf{f}}{\partial x_1} & \cdots & \dfrac{\partial \mathbf{f}}{\partial x_n} \end{bmatrix} = \begin{bmatrix} \dfrac{\partial f_1}{\partial x_1} & \cdots & \dfrac{\partial f_1}{\partial x_n}\\
\vdots & \ddots & \vdots\\
\dfrac{\partial f_m}{\partial x_1} & \cdots & \dfrac{\partial f_m}{\partial x_n} \end{bmatrix}$$

在后文的计算中，对于每个Element，需要将全局点中的点值映射到 Elements 中的内插点中，故需要使用到 Jacobi 矩阵进行变换，对于复杂的几何图形可以通过构建雅克比矩阵映射到形函数上进行计算。

Jacobian Determinant 雅克比行列式：

$$\mathcal{J} = \left|\left|\mathbf J \right|\right|=\left| \frac{\partial(x,y,z)}{\partial(\xi,\eta,\zeta)}\right|$$

可以用以描述每个 Elements的体积变换：

$$ dx dy dz = \mathcal{J} d\xi d\eta d\zeta $$

SEM推导

有了以上数学工具的补充，我们可以开始进行进一步的物理推导；首先对于一维的波动方程有：

$$\rho \frac{\partial^{2} u}{\partial t^{2}}-\frac{\partial}{\partial x}\left(\mu \frac{\partial u}{\partial x}\right)=f(x)$$

使用权函数 $v$，弱形式为：

$$\int_{\Omega} \rho v \ddot{u} d x+\int_{\Omega} \nabla v \mu \nabla u d x=\int_{\Omega} v f d x$$

使用 Jacobian 矩阵将 $x$坐标变换到 $\xi$坐标，对于左边第一项有：

$$\int_{\Omega_{e}} \rho(x) v(x) \ddot{u}(x) d x=\int_{\wedge} \rho(\xi) v(\xi) \ddot{u}(\xi) \mathcal{J} d \xi$$

使用 Legrange 插值 $v$ 和 $u$：

$$=\int _ { -1 }^{ 1 } \rho (\xi )\left. \left[ \sum _ { i=0 }^{ N } v_{ i }\ell _ { i }(\xi ) \right] \left[ \sum _ { j=0 }^{ N } \ddot { u } _ { j }\ell _ { j }(\xi ) \right] { \mathcal{J} }d\xi \right. $$

GLL点权值近似积分，加上 $\omega_i$项：

$$=\sum_{k=0}^{N}\left[\rho\left(\xi_{k}\right) {\omega_{k}}\left(\sum_{i=0}^{N} v_{i} \ell_{i}\left(\xi_{k}\right)\right)\left(\sum_{j=0}^{N} \ddot{u}_{j} \ell_{j}\left(\xi_{k}\right)\right) \mathcal{J}\left(\xi_{k}\right)\right]$$ 将拉格朗日插值函数替换为 Kronecker $\delta$ 函数

$$=\sum_{k=0}^{N}\left[\rho_{k} \omega_{k}\left(\sum_{i=0}^{N} \delta_{i k}\right)\left(\sum_{j=0}^{N} \ddot{u}_{j} \delta_{j k}\right) \mathcal{J}_{k}\right]$$

整理得：

$$=\sum_{j=0}^{N}\left[\ddot{u}_{j}\left(\sum_{i=0}^{N} \sum_{k=0}^{N} \rho_{k} \omega_{k} \delta_{i k} \delta_{j k} \mathcal{J}_{k}\right)\right]$$

令 $m e_{i j}=\rho_{i} \omega_{i} \mathcal{J}_{i} \delta_{i j}$：

$$ = \ddot{u}_ {j} m e _ {ij}=\mathbf{M} \ddot{\mathbf{U}} $$

同样，对于左边第二项也可以有：

$$k e_{i j}=\sum_{k=0}^{N} \mu_{k} \omega_{k} \ell_{i}^{\prime}\left(\xi_{k}\right) \ell_{j}^{\prime}\left(\xi_{k}\right) \mathcal{J}_{k}$$

最终，线性系统求解变为：

$$\mathbf{M} \ddot{\mathbf{U}}+\mathbf{K} \mathbf{U}=\mathbf{F}$$

其中：$\mathbf{M}$ 为 Mass Matrix；$\mathbf{K}$ 为 Stiffness Matrix；$ \mathbf{F} $ 为 Source Matrix。

拓展到三维，对于$f(\mathbf{x})$ ：

$$ \mathbf{u}(\mathbf{x}(\xi, \eta, \zeta), t) \approx \sum_{i, j, k=1}^{n} u_{m}^{i j k}(t) \ell_{i}\left(\xi_{i}\right) \ell_{j}\left(\eta_{j}\right)\ell_{k}\left(\zeta_{k}\right) $$

$$ \mathbf{v}(\mathbf{x}(\xi, \eta, \zeta), t) \approx \sum_{i, j, k=1}^{n} v_{m}^{i j k}(t) \ell_{i}\left(\xi_{i}\right) \ell_{j}\left(\eta_{j}\right)\ell_{k}\left(\zeta_{k}\right) $$

带入有：

$$\int_{V} f(\mathbf{x}) d \mathbf{x}^{3}=\int_{-1}^{1} \int_{-1}^{1} \int_{-1}^{1} f(\mathbf{x}(\xi, \eta, \zeta)) \mathcal{J}(\xi, \eta, \zeta) d \xi d \eta d \zeta \approx \sum_{i, j, k=1}^{n} \omega_{i} \omega_{j} \omega_{k} f_{i j k} \mathcal{J}_{e}^{i j k}$$

对于波动方程左边第一项： $$\int_{V} \rho \mathbf{v} \cdot \ddot{\mathbf{u}} d x^{3}\\ =\sum_{i j k} \omega_{i} \omega_{j} \omega_{k} \rho_{i j k}\left[\left(\sum_{i j k} v_{m}^{i j k} \ell_{i}\left(\xi_{i}\right) \ell_{j}\left(\eta_{j}\right)\ell_{k}\left(\zeta_{k}\right)\right) \cdot\left( \sum_{p q r} \ddot{u}_{n}^{p q r}(t) \ell_{p}\left(\xi_{i}\right) \ell_{q}\left(\eta_{j}\right)\ell_{r}\left(\zeta_{k}\right)\right)\right] \mathcal{J}_{e}^{i j k}$$

$$=\sum_{i j k} \omega_{i} \omega_{j} \omega_{k} \rho_{i j k} \mathcal{J}_{e}^{i j k} \sum_{m, n=1}^{3} \delta_{m n} \sum_{i j k} v_{m}^{i j k} \delta_{i i} \delta_{j j} \delta_{k k} \sum_{p q r} \ddot{u}_{n}^{p q r}(t) \delta_{p i} \delta_{q j} \delta_{r k} $$

$$=\sum_{i j k} \omega_{i} \omega_{j} \omega_{k} \rho_{i j k} \mathcal{J}_{e}^{i j k} \sum_{m=1}^{3} w_{m}^{i j k} \ddot{u}_{m}^{i j k}$$

对于其他项，依次推导，之后同样可以使用三个矩阵表示：

$$\mathbf{M} \ddot{\mathbf{U}}+\mathbf{K} \mathbf{U}=\mathbf{F}$$

装配方法/边界条件等细节待补充。

Python 演示实现

SEM的二维演示：

项目地址

git clone https://github.com/Dongsh/pySEMLAB

基本思路：

GLL Point点获取，网格划分。
设置源、台站以及边界条件。
更新计算整个波场
结果导出

1. 网格/GLL点划分

meshBox.py：

import numpy as np

# 从文件读取得到 GLL point 的划分与权值
def GetGLL(*par):               
    if len(par) > 1:
        kind = par[1]
        prefix = kind[:3]
    else:
        prefix = "gll"
    ngll = par[0]
    name = "gll_xwh/" + prefix + "_" + str(ngll) + ".tab"
    with open(name, 'r') as file:
        array = []
        for line in file:
            array.append([float(x) for x in line.split()])
    file.close()
    x = array[0][:]
    w = array[1][:]
    h = array[2:][:]
    return x, w, h

# 全局网格划分，返回每个Element中GLL点的数组编号，及x, y坐标
def meshBox(LX, LY, NELX, NELY, NGLL):   
    dxe = LX / NELX
    dye = LY / NELY
    XGLL = GetGLL(NGLL)[0]

    iglob = np.zeros([NGLL, NGLL, NELX * NELY + 1])
    nglob = (NELX * (NGLL - 1) + 1) * (NELY * (NGLL - 1) + 1)
    x = np.zeros([nglob, 1])
    y = np.zeros([nglob, 1])
    e = 0
    last_iglob = 0
    igL = np.array(range(1, NGLL * (NGLL - 1) + 1)).reshape([NGLL, NGLL - 1]).T
    igB = np.array(range(1, NGLL * (NGLL - 1) + 1)).reshape([NGLL - 1, NGLL]).T
    igLB = np.array(range(1, (NGLL - 1) * (NGLL - 1) + 1)).reshape([NGLL - 1, NGLL - 1]).T
    xgll = np.tile([0.5 * (x + 1) for x in XGLL], [1, NGLL]).reshape([NGLL, NGLL]).T
    ygll = dye * xgll.T
    xgll = dye * xgll

    for ey in range(NELY):
        for ex in range(NELX):
            e = e + 1

            if e == 1:
                ig = np.array(range(0, NGLL * NGLL)).reshape([NGLL, NGLL]).T+1
            else:
                if ey == 0:

                    ig[0, :] = iglob[NGLL - 1, :, e - 1]  # left edge
                    ig[1:NGLL, :] = last_iglob + igL
                elif ex == 0:

                    ig[:, 0] = iglob[:, NGLL - 1, e - NELX]
                    ig[:, 1:NGLL] = last_iglob + igB

                else:
                    ig[0, :] = iglob[NGLL - 1, :, e - 1]
                    ig[:, 0] = iglob[:, NGLL - 1, e - NELX]
                    ig[1:NGLL, 1:NGLL] = last_iglob + igLB

            iglob[:, :, e] = ig
            last_iglob = ig[NGLL - 1, NGLL - 1]
            x[ig - 1] = dxe * ex + xgll[:, :, np.newaxis]
            y[ig - 1] = dye * ey + ygll[:, :, np.newaxis]

    iglob = iglob[:, :, 1:NELX * NELY + 1]
    return iglob, x, y

主程序 main.py

import numpy as np
import meshBox
import Boundary
import Friction
import matplotlib.pyplot as plt

if __name__ == '__main__':
    LX = 12.5e3
    LY = 7.5e3

    NELX = 25
    NELY = 15
    P = 4  # Polynomial Degree

    ABC_B = 0
    ABC_R = 2
    ABC_T = 2
    ABC_L = 0

    dxe = LX / NELX
    dye = LY / NELY
    NEL = NELX * NELY
    NGLL = P + 1
    
    # 获取GLL Point，构建全局Elements划分
    iglob, x, y = meshBox.meshBox(LX=LX, LY=LY, NELX=NELX, NELY=NELY, NGLL=NGLL)

    nglob = len(x)

    RHO = 2670.
    VS = 3464.
    MU = RHO * VS ** 2

    ETA = 0.1
    PML_A = 10
    PML_N = 2

    xgll, wgll, H = meshBox.GetGLL(NGLL)
    

    Ht = np.array(H).T
    W = np.array(wgll)[:, np.newaxis] * np.array(wgll)[np.newaxis, :]
    M = np.zeros([nglob, 1])
    rho = np.zeros([NGLL, NGLL])
    mu = np.zeros([NGLL, NGLL])
    NT = 0
    TT = 12
    CFL = 0.6

    dt = np.inf
    dx_dxi = 0.5 * dxe
    dy_deta = 0.5 * dye
    jac = dx_dxi * dy_deta
    coefint1 = jac / dx_dxi
    coefint2 = jac / dy_deta

    # 对每个Elements内的参数进行设定
    for ey in range(NELY):
        for ex in range(NELX):
            e = (ey) * NELX + ex-1
            ig = iglob[:, :, e].astype(np.int32) - 1

            rho[:, :] = RHO
            mu[:, :] = MU

            M[ig] = M[ig] + (np.multiply(W, rho) * jac)[:, :, np.newaxis]
            vs = np.sqrt(mu / rho)
            if dxe < dye:
                vs = np.maximum(vs[0:NGLL - 1, :], vs[1:NGLL, :])
                dx = meshBox.repmat(np.diff(xgll) * 0.5 * dxe, 1, NGLL)
            else:
                vs = np.maximum(vs[:, 0:NGLL - 1], vs[:, 1:NGLL])
                dx = meshBox.repmat(np.diff(xgll).T * 0.5 * dxe, NGLL, 1)

            dtloc = dx / vs

            dt = np.min(np.append(np.array(dtloc.flatten(order='F')), np.array(dt)))

    dt = CFL * dt

    
    f = np.zeros([nglob, 1])
    v = np.zeros([nglob, 1])
    d = np.zeros([nglob, 1])

2. 震源、台站及边界条件设定：

main.py

 anyPML = np.array(np.array([ABC_T, ABC_R]) == 2).any()
    if anyPML:

        ePML = []
        NEL_PML = 0
        if ABC_R > 1:
            ePML = np.arange(NELX, NEL + 1, NELX)
        if ABC_T > 1:
            ePML = np.append(ePML, range(NEL - NELX, NEL))
        ePML = np.unique(ePML)
        NEL_PML = len(ePML)
        iglob_PML = iglob[:, :, ePML - 1]
        
        iPML, dum, iglob_PML = np.unique(iglob_PML.flatten(order='F'), return_index=True, return_inverse=True)
        iglob_PML = iglob_PML.reshape([NGLL, NGLL, NEL_PML],order='F')
        nPML = len(ePML)
        axPML = np.zeros([nPML, 1])
        ayPML = np.zeros([nPML, 1])

        xp = x[iPML.astype(int) - 1]
        yp = y[iPML.astype(int) - 1]
        lx = LX - dxe
        ly = LY - dye

        if ABC_R:
            axPML = PML_A * VS / dxe * ((xp - lx) / dxe) ** PML_N * (xp >= lx)
        if ABC_T:
            ayPML = PML_A * VS / dye * ((yp - ly) / dye) ** PML_N * (yp >= ly)


        ahsumPML = 0.5 * (axPML + ayPML)
        aprodPML = axPML * ayPML
        asinvPML = 1 / (1 + dt * ahsumPML)

        s_x = np.zeros([NGLL, NGLL, NEL_PML])
        s_y = np.zeros([NGLL, NGLL, NEL_PML])
    else:
        NEL_PML = 0
        ePML = 0
        # iglob_PML = iglob[:, :, ePML]

    # 震源设置
    FltB, iFlt, noUsed = Boundary.BoundaryMatrix(wgll=wgll, NELXY=[NELX, NELY], iglob=iglob, jac1D=dx_dxi, side='B')


    FltN = len(iFlt)
    FltZ = np.array(M[iFlt.astype(int)-1].squeeze() / FltB.T).squeeze() / dt
    FltX = x[iFlt.astype(int)]
    FltV = np.zeros([FltN, NT.astype(int)])
    FltD = np.zeros([FltN, NT.astype(int)])
    # # % background stress
    FltNormalStress = 120e6
    FltInitStress = meshBox.repmat(70e6, FltN, 1)
    # % nucleation
    isel = np.where(np.abs(np.array(FltX).squeeze()) <= 1.5e3)  # isel = find(abs(FltX) <= 1.5e3);
    # print(np.array(FltX).squeeze())
    FltInitStress[isel] = 81.6e6
    # % friction
    FltFriction = Friction.Friction()
    FltState = np.zeros([1, FltN])
    FltFriction.MUs = meshBox.repmat(0.677, FltN, 1)
    FltFriction.MUd = meshBox.repmat(0.525, FltN, 1)
    FltFriction.Dc = 0.4
    # # % barrier
    L_BARRIER = 15e3 / 2
    # # isel = find(abs(FltX) > L_BARRIER);
    isel = np.where(np.abs(np.array(FltX).squeeze()) > L_BARRIER)  # isel = find(abs(FltX) > L_BARRIER);
    FltFriction.MUs[isel] = 1e4
    FltFriction.MUd[isel] = 1e4
    FltFrictionW = (FltFriction.MUs - FltFriction.MUd) / FltFriction.Dc
    FltStrength = Friction.friction(u=FltState, f=FltFriction) * FltNormalStress - FltInitStress  # strength excess

    if ETA:

        NEL_ETA = min(np.float(NELX), np.ceil(L_BARRIER / dxe) + 2)
        x1 = 0.5 * (1 + np.array(xgll).T)
        eta_tapper = np.exp(-np.pi * x1 ** 2)
        eta = ETA * dt * meshBox.repmat(eta_tapper, NGLL, 1)
    else:
        NEL_ETA = 0
    
    # 台站设定
    OUTxseis = np.arange(0, 10e3 + 1, 0.5e3).T
    OUTnseis = len(OUTxseis)
    OUTyseis = meshBox.repmat(2e3, OUTnseis, 1)

    OUTxseis, OUTyseis, OUTiglob, OUTdseis = meshBox.FindNearestNode(xin=OUTxseis, yin=OUTyseis, X=x, Y=y)
    OUTv = np.zeros([OUTnseis, NT.astype(int)])
    OUTdt = np.floor(0.5 / dt)
    OUTit = 0

3/4. 方程迭代求解与结果输出

main.py

 # Solve Equation
    
    for it in range(0, int(NT)):
        d = d + dt * v
        FltD[:, it] = 2 * d[iFlt.astype(int)-1].squeeze()

        f[:] = 0

        ep = 0
        # eep = ePML[ep]
        eep = ePML[ep]

        # eepn = eN

        for e in range(NEL):
            isPML = e == eep
            isETA = e <= NEL_ETA

            ig = iglob[:, :, e]

            if isPML:
                igPML = iglob_PML[:, :, ep]
                ax = axPML[igPML.astype(int) - 1]
                ay = ayPML[igPML.astype(int) - 1]

                vloc = v[ig.astype(int) - 1]
                dloc = d[ig.astype(int) - 1] - half_dt * vloc
                locx = vloc + np.multiply(ay, dloc)
                locy = vloc + np.multiply(ax, dloc)

                sx = MU * Ht * locx.squeeze() / dx_dxi
                sy = MU * locy.squeeze() * H / dy_deta
                sx = np.multiply(dt * sx + (1 - half_dt * ax).squeeze(), s_x[:, :, ep]) / (1 + half_dt * ax).squeeze()
                sy = np.multiply(dt * sy + (1 - half_dt * ay).squeeze(), s_y[:, :, ep]) / (1 + half_dt * ay).squeeze()

                s_x[:, :, ep] = sx
                s_y[:, :, ep] = sy

                ep = ep + 1
                if ep <= NEL_PML:
                    eep = ePML[ep]
                else:
                    eep = 0

            else:
                if isETA:
                    local = d[ig.astype(int) - 1].squeeze() + np.multiply(eta, v[ig.astype(int) - 1].squeeze())
                else:
                    local = d[ig.astype(int) - 1]
                

                sx = MU * np.dot(Ht, local.squeeze()) / dx_dxi
                sy = MU * np.dot(local.squeeze(), H) / dy_deta
                
                
            d_xi = W * sx
            d_xi =np.dot( H, d_xi )* coefint1
            d_eta = W * sy
            d_eta =coefint2* np.dot(d_eta , Ht )
            local = d_xi + d_eta
#            print(np.max(local))

#            f[ig.astype(int) - 1] = (f[ig.astype(int) - 1].squeeze() - local)[:, :, np.newaxis]
            f[ig.astype(int).flatten(order='F') - 1] = (f[ig.astype(int).flatten(order='F') - 1].squeeze() - local.flatten(order='F'))[:, np.newaxis]
            
        if ABC_L == 1:
            f[iBcL-1] = f[iBcL-1] - np.multiply(BcLC, v[iBcL-1])
        if ABC_R == 1:
            f[iBcR-1] = f[iBcR-1] - np.multiply(BcRC, v[iBcR-1])
        if ABC_T == 1:
            f[iBcT-1] = f[iBcT-1] - np.multiply(BcTC, v[iBcT-1])

        if anyPML:
            tmp = np.multiply(ahsumPML, v[iPML.astype(int) - 1].T) + np.multiply(aprodPML, d[iPML.astype(int) - 1])
            f[iPML.astype(int) - 1] = np.multiply(aprodPML.squeeze(), d[iPML.astype(int) - 1].squeeze())[:, np.newaxis]

        FltState = np.maximum(FltD[:, it], FltState)
        FltStrength = (Friction.friction(FltState.T, FltFriction) * FltNormalStress).squeeze() - FltInitStress.squeeze()
        FltVFree = v[iFlt.astype(int)-1].squeeze() + dt * f[iFlt.astype(int)-1].squeeze() / M[iFlt.astype(int)-1].squeeze()

        # raise RuntimeError('Stop')
        TauStick = np.multiply(FltZ, FltVFree)

        Tau = np.minimum(TauStick, FltStrength)

        f[iFlt.astype(int)-1] = (f[iFlt.astype(int)-1].squeeze() - np.multiply(FltB.squeeze(), Tau).squeeze())[:, np.newaxis, np.newaxis]

        v = v + dt * f / M

        # if anyPML
        FltV[:, it] = 2 * v[iFlt.astype(int)].squeeze()

        # STEP 4 OUT

        OUTv[:, it] = v[OUTiglob.astype(int)].squeeze()

        if np.mod(it, OUTdt) == 0:
            OUTit = OUTit + 1

            # FIGURE 1

            # FIGURE 2

            # test[it] = max(abs(v))
        plt.cla()
        plt.scatter(x,y,c=v)
        plt.pause(0.0001)