伪谱法 Pseudo-spectral method 初探及 Python 实现

2020.08.08

伪谱法（Pseudo-spectral method）是一种求解偏微分方程(PDE)的常见方法，本文初步讨论使用傅里叶展开的伪谱法的推导与实现。

推导

一维对流方程

$$\frac{\partial u}{\partial t} + c \frac{\partial u}{\partial x} = 0 $$

取 $c = 1$，目标为用伪谱法求解：

$$\frac{\partial u}{\partial t} + \frac{\partial u}{\partial x} = 0 $$

初场（源）为 $ u_0(x)=e^{-x^2} $, $x\in [-5,5]$

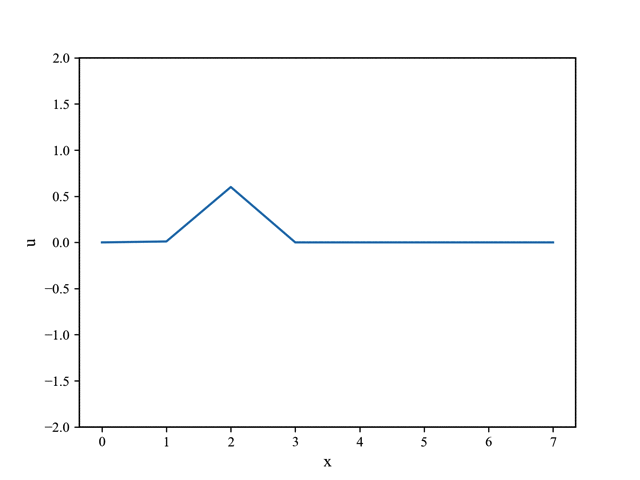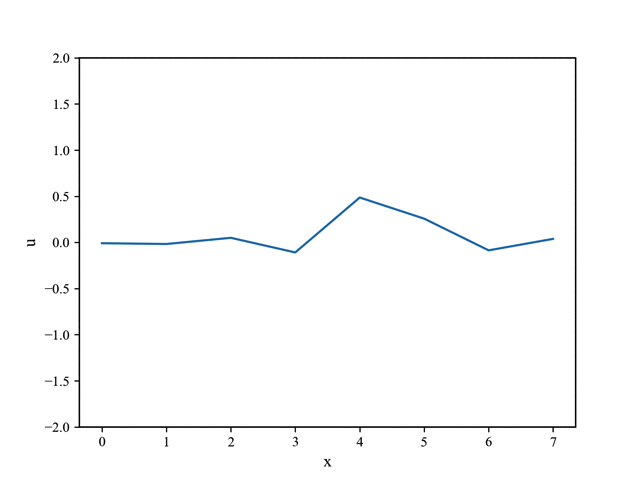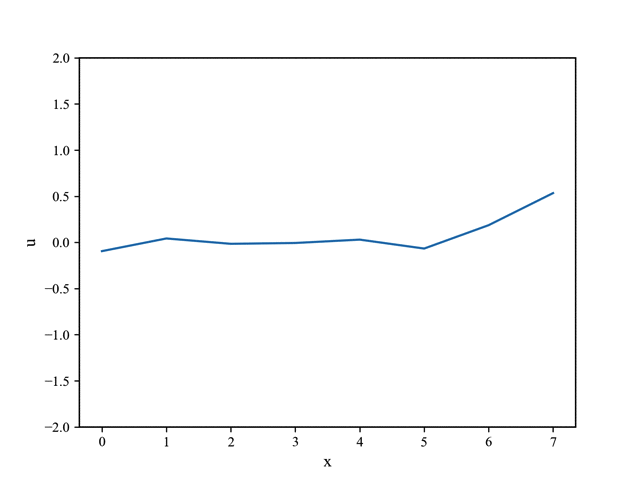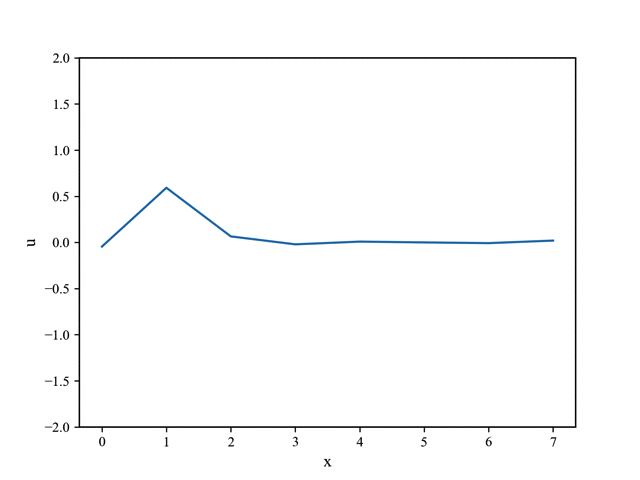
空间精度取 $8$ 阶，时间推进使用欧拉法，步长取 $0.1$。

首先构造推进使用的离散方程

傅里叶展开 $u$:

$$u(x,t) = \sum a_i(t)e^{j\omega_ix}$$

带入原方程：

$$ \frac{\partial \sum a_i(t)e^{j\omega_ix}}{\partial t} + \frac{\partial \sum a_i(t)e^{j\omega_ix}}{\partial x} = 0 $$

推导：

$$ \frac{\partial \sum a_i(t)e^{j\omega_ix}}{\partial t} + \sum j \omega_i a_i(t)e^{j\omega_ix} = 0 $$

第一项（时间项）继续使用 Runge-Kutta法近似有：

$$ \frac{\partial \sum a_i(t)e^{j\omega_ix}}{\partial t} = \sum \frac{a_i^{n+1}-a_i^{n}}{\Delta t} e^{-j\omega_ix}$$

带入公式有：

$$ \sum \frac{a_i^{n+1}-a_i^{n}}{\Delta t} e^{-j\omega_ix} + \sum j \omega_i a_i(t)e^{j\omega_ix} = 0 $$

得到谱更新公式：

$$ a^{n+1}_i = (1-j\Delta t \omega_i)a^n_i$$

其中谱更新公式中的系数$(1-j\Delta t \omega _i)$有 $|(1-j\Delta t \omega_i)| > 1$，会导致谱系数不断增大导致输出高频振荡计算不稳定，故使用：

$$ a^{n+1}_i = \frac{(1-j\Delta t \omega_i)}{|(1-j\Delta t \omega_i)|}a^n_i$$

为实际的谱更新函数。

Python实现

import numpy as np
import matplotlib.pyplot as plt
from dsPltTool import *

N = 8               # 阶数
NT = 200            # 计算时间迭代

rb = -5             # 左右边界
l = 20

dt = 0.1            # 时间步长
delay = 0.0001      # 绘图延迟

def init_guass():   # 计算初场
	u0 = np.zeros(N)
	for ii in range(N):
		u0[ii] = np.exp(-(l*ii/(N-1)+rb)**2)
		
	return u0
	
def advance(us):    # 更新函数
	for ii in range(int(N/2)+1):
		us[ii] = ((1+0j) - (ii*dt*(2*np.pi/l)+0j) * (0+1j))/abs(((1+0j) - (ii*dt*(2*np.pi/l)+0j) * (0+1j))) * us[ii]

	return us
	
		
if __name__ == "__main__":
	us = (1+0j)*np.zeros(N)
	
	up = init_guass()
	us = np.fft.rfft(up)   
	plt.cla()
	plt.plot(up)
	mst(label=['x','u'], ylim=[-2,2])
	plt.pause(delay)
	
	for ii in range(NT):
		print(ii)
		us = advance(us)
		up = np.fft.irfft(us);
		plt.cla()
		plt.plot(np.real(up))
		mst(label=['x','u'], ylim=[-2,2])
		plt.pause(delay)

使用 numpy.fft.rfft 实现由实数域到复数域的傅里叶变换，参考：Numpy 中 fft() 与 rfft() 的区别

可以得到输出：

提升阶数N到 $80$（加密空间网格），可以得到：

一维声波方程

推导

$$ \frac{1}{\rho c^2} \frac{\partial ^2 P}{\partial t^2} = \frac{\partial }{\partial x}\left(\frac{1}{\rho}\frac{\partial P}{\partial x}\right) $$

左侧时间项使用二阶差分近似：

$$ \frac{1}{\rho c^2} \frac{1}{(dt)^2} \left[ P(t+dt) - 2P(t) + P(t-dt)\right] =\frac{\partial }{\partial x}\left(\frac{1}{\rho}\frac{\partial P}{\partial x}\right)$$

得到时间更新/步进公式：

$$ P(t+dt) = \rho c^2 (dt)^2 \frac{\partial }{\partial x}\left(\frac{1}{\rho}\frac{\partial P}{\partial x}\right) + 2P(t) - P(t-dt)$$

对于空间微分$\frac{\partial }{\partial x}\left(\frac{1}{\rho}\frac{\partial P}{\partial x}\right) $ ，使用两次傅里叶积分：

$$ \frac { \partial f(x) }{ \partial x } =\frac { \int _{ -\infty }^{ \infty }{ F(k)e^{ -ikx } } dk }{ \partial k } =-\int _{ -\infty }^{ \infty }{ ikF(k)^{ -ikx }dk } $$

即可使用 $ P _ j ^ n $ 计算出$\frac{\partial }{\partial x}\left(\frac{1}{\rho}\frac{\partial P}{\partial x}\right) $：

$$P_{ j }^{ n }\xrightarrow { \text{FFT} } \hat { P } _{ v }^{ n }\rightarrow ik_{ v }\hat { P } _{ v }^{ n }\xrightarrow { \text{rFFT} } \frac { \partial P^{ n }_{ j } }{ \partial x } \ \\ \xrightarrow { \cdot 1/\rho } \frac { 1 }{ \rho } \frac { \partial P^{ n }_{ j } }{ \partial x } \xrightarrow { \text{FFT} } \left( \frac { 1 }{ \rho } \frac { \partial P^{ n }_{ j } }{ \partial x } \right) ^{ n }_{ v }\rightarrow ik_{ v }\left( \frac { 1 }{ \rho } \frac { \partial P^{ n }_{ j } }{ \partial x } \right) ^{ n }_{ v }\xrightarrow { \text{rFFT} } \frac { \partial }{ \partial x } \left( \frac { 1 }{ \rho } \frac { \partial P^{ n }_{ j } }{ \partial x } \right) $$

Python 实现

为方便取 $\rho = 1$，$c = 1$ 进行实现：

import numpy as np
import matplotlib.pyplot as plt
from dsPltTool import *

N = 80
NT = 200

rb = -5
l = 20

dt = 0.1
delay = 0.001

def init_guass():
	u0 = np.zeros(N)
	for ii in range(N):
		u0[ii] = np.exp(-(l*(ii)/(N-1)-2)**2)
		
	return u0

def advance(us):
	for ii in range(int(N/2)+1):
		us[ii] = (-(ii*dt*(2*np.pi/l)+0j) * (0+1j)) * us[ii]

	return us
			
if __name__ == "__main__":
	us = (1+0j)*np.zeros(N)
	
	up = init_guass()
	us = np.fft.rfft(up)
	plt.cla()
	plt.plot(up)
	mst(label=['x','u'], ylim=[-2,2])
	plt.pause(delay)
	upOld = up
	upNow = up
	for ii in range(NT):
		print(ii)
		
		us = advance(us)
		us = advance(us)
		up = np.fft.irfft(us) + 2 * upNow - upOld
		plt.cla()
		
		plt.plot(np.real(up))
		mst(label=['x','u'], ylim=[-2,2])
		plt.pause(delay)
		
		us = np.fft.rfft(up)

		upOld = upNow
		upNow = up